３．探索法

対象となる問題をうまく探索木（又は有向グラフ）として表現できたら今度はその探索木を以下に効率よく調べるかが問題になります。これが探索の問題です。探索には節点を一つずつ調べていく必要がありますが、ゴール（求めたい解）にたどりつくまでになるべく少ない計算量で行くことができればよりいい探索法となります。（当たり前ですね。）つまり、より効率の良い順番で節点を調べていく方法が、良い探索法というわけです。

以下で扱う探索法は、探索木に対して何の予備知識も使わずに探索を行う単純な探索（ブラインド探索）と何らかの知識を用いた探索（ヒューリスティック探索）の２種類があります。

単純な探索法　（ブラインド探索）　blind search

知識を用いない単純な探索法の中でも、もっとも基本的なものに縦形探索と横形探索があります。この二つの方法は非常に単純なアルゴリズムなので作るのも簡単ですが、当然性能もそれなりです。

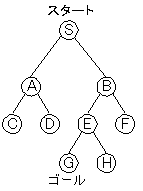
図３．１　探索木の例 縦形探索　（深さ優先探索）　DFS : depth-first search

枝を先に進めるかぎり掘り進めて、行き詰まったら次の枝を調べるという方法が縦形探索です。図３．１の探索木に対して探索を行う場合について考えてみます。
先に探索結果を示してしておくと、

Ｓ→Ａ→Ｃ→Ｄ→Ｂ→Ｅ→Ｇ

という順番に節点を調べていきます。

縦形探索では木の深さを優先して探索を行うわけですから、現在開いている（現在調べた）節点に子節点があるなら、そちらの節点を先に調べていきます。探索はＳから始まるわけですが、ＳにはＡとＢの二つの子節点があります。ここでは、開く条件の同じ節点が複数ある場合には、便宜上アルファベットの若い順に調べることにします。

そうすると、Ｓの次にはＡが開かれることになります。するとＡにはＣとＤの二つの子節点があるのでさらに深く進んで、Ｃを調べます。今度はＣには子節点がなく、またＣはゴールではないので、一つ戻ってＡのもう一つの子節点であるＤを調べます。しかし、Ｄにも子節点はなくゴールでもないので、Ｓまで戻ってＢを開きます。すると子節点ＥとＦが見つかります。そこでアルファベット順にＥを開いてみると、ＧとＨが子節点にあることがわかります。そこで、さらに深く進んで、Ｇを開いて見るとこれが目的のゴールにあたる節点だとわかります。これで探索は終了です。

今回の例では、ＦとＨは調べずに済みました。しかしあまり効率が良いとはいえませんね。

もう少しわかりやすいように、openリストとcloseリストを書いてみましょう。openリストとは、現在開くことのできる節点のリストで、通常このリストで前にあるものから開かれます。closeリストとは開いて調べてしまった節点のリストで、調べおわった状態を閉じるとして、closeリストといいます。

open (S)→(AB)→(CDB)→(DB)→(B)→(EF)→(GHF)
close ( )→(S)→(AS)→(CAS)→(DCAS)→(BDCAS)→(EBDCAS)

横形探索　（幅優先探索）　BFS : breadth-first search

同じ深さの節点を調べ終わってから次の深さに進むというのが横形探索です。図３．１の探索木に対して横形探索を行ってみます。
探索結果は、

Ｓ→Ａ→Ｂ→Ｃ→Ｄ→Ｅ→Ｆ→Ｇ

となります。openリストとcloseリストは次のようになります。

open (S)→(AB)→(BCD)→(CDEF)→(DEF)→(EF)→(FGH)→(GH)
close ( )→(S)→(AS)→(BAS)→(CBAS)→(DCBAS)→(EDCBAS)→(FEDCBAS)

Ｓの子節点はＡとＢなので、まずＡが開かれます。すると子節点はＣとＤが見つかるので、これはopenリストのＢの後ろに追加されます。次にopenリストで一番前にあるのはＢなので今度はＢが開かれます。ここで、ＥとＦが出てくるのでこれをopenリストの後ろに追加します。このように、横形探索では先に出てきたものほど先に開かれます。このため、図３．１のような探索木なら、アルファベット順に開かれていきます。

今回の例では縦形探索のほうが横形探索よりも一手少なくゴールにたどりついています。一般に探索木は深いがゴールは浅いところにある場合は横形探索のほうが効率がいいといわれています。

ところで、アルゴリズム（データ構造）に詳しい人には、縦形探索はスタックで横形探索はキューだと言うとわかりやすいでしょうか？

知識を用いた探索　（ヒューリスティック探索）

探索木や、有向グラフに何らかのコストというものがわかる場合には、これを利用して探索を行うことが考えられます。例えば、積み木の問題では積み木を動かすのにかかる時間であるとかエネルギーといったものは、状態（各状態が節点にあたります）を変化させるために使われるコストというように考えることができます。とくに、ある状態から目的の状態へ変化させるまでに、複数の方法があるようなときには、どのような経路をたどって、目的の状態へ持っていくかということが、探索の重要な目的となるわけです。

積み木の問題なら、単純に手数が少なく目的の積み方に導けるほうがいいですし、迷路を解く問題ならなるべく短い経路を通ってゴールまで行くほうがいいですね。

コストがわかる場合、状態を変化させるのにかかるコストがわかる場合（つまり枝のコストがわかるということです。）とそれぞれの節点から目的の状態（ゴール）までのコストが予測できる場合の２種類が考えられます。平たく言うと、スタートからのコストの履歴がわかる場合と、各地点でのゴールまでのコストが予測できる場合ということになりますね。もちろん両方わかる場合も考えられます。

分岐限定法　（最適解の探索）　branch and bound (optimal-search)

まずは、各枝のコストがわかる場合について考えてみます。このような場合、コストの最少となる経路を見つけることができます。各節点を開き子節点をopenリストに入れるときに、そこまでの経路のコストを使って、コストの小さいものが前に来るようにopenリストを並べ直してやると、そこまででコストの一番小さな経路が常に選択されることになります。つまり、余計な節点を開く可能性は高いものの、最後に得られる経路が最適なものになるというのが分岐限定法です。

分岐限定法の特徴として、有向グラフのようにゴールまでに複数の経路を選べるような場合でも、コスト最少の経路を見つけることができます。なぜなら、コストが高くopenリスト中で後ろのほうにある節点でも、そこまでの新しい経路が見つかったとき、その経路のほうがコストが低ければ、新しい経路をその節点への道として記録し直します。このため、openリストに入っている節点までのコストは、常にその時点での最少のコストになり、ゴールにたどりついたときには、ゴールまでの最少のコストが求まっているというわけです。

一言で言うと分岐限定法は節点までのコストを保持し、そのコストが最少になる節点を次に展開していくアルゴリズムです。

それでは例を挙げてみます。

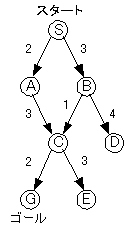
図３．２　有向グラフの例
（※枝の横にある数字がその枝のコストです）

図３．２のような有向グラフに対して分岐限定法を用いると、openリストは

[S(0)]→[A(3),B(3)]→[B(3),C(5)]→[C(4),D(7)]→[G(6),D(7),E(7)]

となります。

Ｓを展開するときには「Ａの親はＳ」「Ｂの親はＳ」という情報を記録します。また、Ｃのような場合には、Ａが展開されたときに「Ｃの親はＡ」と記録されそのとき、Ｃへのコストは５と記録されますが、この後、Ｂが展開されるとコストが４でＣにたどり着くので、「Ｃの親はＢ」と書き換えられます。そして、Ｃへのコストが一番小さいのでＣが展開され、続いてＧが展開されます。ここで、Ｇの親はＣで、Ｃの親はＢ、その親はＳなので、

Ｓ→Ｂ→Ｃ→Ｇ

という経路がもっともコストの低い経路として導かれます。

枝のコストがわかっている場合には分岐限定法は常に最適な経路を発見できます。

次に各節点からゴールまでのコストが予測できる場合に使える手法を紹介します。

山登り法　（勾配降下法）　hill climbing ( gradient descent )

山登り法は非常に単純なアルゴリズムで、現在の節点の子節点全てについて、ゴールまでの予測コストがもっとも低いものを選択し、その節点を開きその子節点の中で一番コストの低いものを･･･というものです。この方法は、その時目の前にあるもののうち一番良いものを選びつづけるアルゴリズムといえます。このため、問題の性質によっては、最適な答えどころか答えまで行き着けないという場合すらあります。

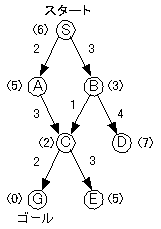
図３．３　予測コストのある有向グラフの例
（※節点の横にある括弧のついた数字がその節点の予測コストです）

openリストは

[S(6)]→[B(3),A(5)]→[C(2),D(7)]→[G(0),E(5)]

となります。

この例は予測コストが実際のコストと一致しているため、得られる経路も
Ｓ→Ｂ→Ｃ→Ｇ
となっていて、山登り法がうまくいく例ですが、予測コストが間違っていてＢの予測コストが６になっていたりするとopenリストは
[S(6)]→[A(5),B(6)]→[C(2)]→[G(0),E(5)]
で、得られる経路は
Ｓ→Ａ→Ｃ→Ｇ
となり、最適な経路ではありません。最悪の場合にはいつまでも同じ場所をループしてしまう可能性すらあります。

最良優先探索　best-first search

山登り法では選択されなかった節点の情報はそのまま廃棄されていましたが、この節点の情報も保持しつづけて今までで一番よさそうな節点を選ぶようにしたのが最良優先探索です。最良優先探索では節点を開き子節点が見つかったときに、その節点が今までに開いたものかどうかもチェックするので（openリストとcloseリストを調べる）山登り法のようにループに陥ってしまうこともありません。しかし、予測コストに依存しているため、やはり最適経路が見つかる保証はありません。

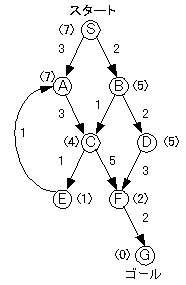
図３．４　ループの可能性のある有向グラフの例

図３．４は山登り法ではループを起こしてしまう例です。これに対して最良優先探索を行うとループに陥らずにゴールまでたどり着くことができます。

山登り法のopenリスト
[S(7)]→[B(5),A(7)]→[C(4),D(5)]→[E(1),F(2)]→[A(7)]→[C(4)]...ループ

最良優先探索のopenリスト
[S(7)]→[B(5),A(7)]→[C(4),D(5),A(7)]→[E(1),F(2),D(5),A(7)]→[F(2),D(5),A(7)]→[G(0),D(5),A(7)]

山登り法ではＡ→Ｃ→Ｅ→Ａというループを回り続けてしまいますが、最良優先探索では、
Ｓ→Ｂ→Ｃ→Ｆ→Ｇ　コスト：１０
という経路を見つけてゴールまでたどり着くことができました。

しかし、ここで有向グラフのコストに注意してみると本当の最適経路は
Ｓ→Ｂ→Ｄ→Ｆ→Ｇ　コスト：９
という経路です。これは実際のコストと予測コストの間にズレがあるために選択できなかった経路です。しかし実際の問題でコストを完全に予測することは難しく最良優先探索ではこのあたりが限界のようです。

ＡアルゴリズムとＡ＊アルゴリズム　algorithm A , algorithm A*

最良優先探索では目標（ゴール）までの予測コストはスタートから現在の節点までのコストは考慮していませんでした。そこで、節点からゴールまでのコストの予測値とスタートから節点までのコストの和を使って、経路の評価を行います。つまり、分岐限定法と最良優先探索の両方の特性を持っている手法です。

また、ＡアルゴリズムとＡ＊アルゴリズムの違いは、予測コストが条件を満たしているかという点だけです。予測コストが実際のコストと比べて、等しいかまたは、実際よりも小さく予測されている場合にはＡ＊アルゴリズムといいます。それ以外の場合はＡアルゴリズムとなります。

Ａアルゴリズムは、最適解が求まる保証はありませんが、Ａ＊アルゴリズムの条件を満たしている場合には、最適解が求まることが保証されています。

このアルゴリズム（ＡまたはＡ＊）は簡単に言うと、最良優先探索で評価に節点の予測コストを用いていたところを、節点の予測コストに、分岐限定法の手法で求めたその節点までのコストをたしたものを代入して、コストの小さいものを選ぶという手法です。ただし、もう一つ違う点があり、一度展開してcloseリストに入れられた節点でも評価コストを保持し、新しく見つかった経路による評価コストがcloseリスト　のものより小さければ、その節点を再びopenリストに入れます。こうすることで最適解が得られることを保証しています。

図３．４は予測コストが実際のコストと等しいか小さいという条件をみたいしているので、これにＡ＊アルゴリズムを適用すると、openリストは

[s(7)]→[B(7),A(10)]→[C(7),D(9),A(10)]→[E(5),D(9),A(10),F(10)]→[D(9),A(10),F(10)]→[F(9),A(10)]→[G(9),A(10)]

となり、６手で最適経路である
Ｓ→Ｂ→Ｄ→Ｆ→Ｇ　コスト：９
が得られます。

さて、ここでＡ＊アルゴリズムの条件が予測コストが実際と等しいかそれより小さいというものでしたが、これはどういうことか例を挙げてみたいと思います。

例えば、図３．５のような迷路でスタートからゴールまでの経路を探索するとき、コストを経路の長さとして、予測コストは座標から縦の距離と横の距離の和とすると、Ａ＊の条件は常に満たされます。ただし、この場合、現在の座標がわかる必要がありますが。

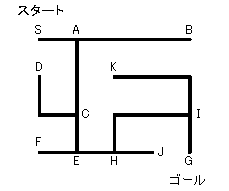
図３．５　迷路の探索の例

実際に値を出してみると、Ｂは予測コストは縦に一直線で３となりますが、実際のコストはＡＣＥＨＩＧとたどる必要があるので、１１となります。Ｃなら予測コストは縦１と横３で合計４となりますが、実際はＥＨＩＧとたどるので、６となります。この二つの例は実際より小さくなりますが、ＫやＩは予測コストが４と１、実際のコストも４と１というように一致しています。しかし、どの節点も予測コストが実際のコストを上回ることはありません。したがって、この例はＡ＊の条件を満たしており、Ａ＊アルゴリズムにより、最適解を求めることができます。

例題

図３．６の有向グラフに対して各探索法を適用した結果を示します。

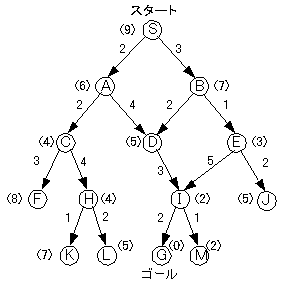
図３．６　大きめの有向グラフ

縦形探索
(S)→(A,B)→(C,D,B)→(F,H,D,B)→(H,D,B)→(K,L,D,B)→(L,D,B)→(D,B)→(I,B)→(G,H,B)
ゴールまでに展開した節点　１０
得られた経路は　Ｓ→Ａ→Ｄ→Ｉ→Ｇ
経路のコストは　１１

横形探索
(S)→(A,B)→(B,C,D)→(C,D,E)→(D,E,F,H)→(E,F,H,I)→(F,H,I,J)→(H,I,J)→(I,J,K,L)→(J,K,L,G,H)→(K,L,G,H)→(L,G,H)→(G,H)
ゴールまでに展開した節点　１３
得られた経路は　Ｓ→Ａ→Ｄ→Ｉ→Ｇ
経路のコストは　１１

分岐限定法
[S(0)]→[A(2),B(3)]→[B(3),C(4),D(6)]→[C(4),E(4),D(5)]→[E(4),D(5),F(7),H(8)]→[D(5),J(6),F(7),H(8),I(9)]→[J(6),F(7),H(8),I(8)]→[F(7),H(8),I(8)]→[H(8),I(8)]→[I(8),K(9),L(10)]→[K(9),M(9),L(10),G(10)]→[M(9),L(10),G(10)]→[L(10),G(10)]→[G(10)]
ゴールまでに展開した節点　１４
得られた経路は　Ｓ→Ｂ→Ｄ→Ｉ→Ｇ
経路のコストは　１０

山登り法
[S(9)]→[A(6),B(7)]→[C(4),D(5)]→[H(4),F(8)]→[L(5),K(7)]→[ ]失敗
Ｃの予測コストがＤのものより小さいために失敗した。

最良優先探索
[S(9)]→[A(6),B(7)]→[C(4),D(5),B(7)]→[H(4),D(5),B(7),F(8)]→[D(5),L(5),B(7),K(7),F(8)]→[I(2),L(5),B(7),K(7),F(8)]→[G(0),M(3),L(5),B(7),K(7),F(8)]
ゴールまでに展開した節点　７
得られた経路は　Ｓ→Ａ→Ｄ→Ｉ→Ｇ
経路のコストは　１１

Ａ＊アルゴリズム
[S(9)]→[A(8),B(10)]→[C(8),B(10),D(11)]→[B(10),D(11),H(12),F(15)]→[E(7),D(10),H(12),F(15)]→[D(10),I(11),J(11),H(12),F(15)]→[I(10),J(11),H(12),F(15)]→[G(10),M(10),J(11),H(12),F(15)]
ゴールまでに展開した節点　８
得られた経路は　Ｓ→Ｂ→Ｄ→Ｉ→Ｇ
経路のコストは　１０

コスト最良の経路を導けたのは分岐限定法とＡ＊アルゴリズムのみで、Ａ＊アルゴリズムのほうが、かなり少ない手数で見つけています。ただし、予測コストが実際のコストに完全に一致しているのなら、余計な計算をしない山登り法が最速となります。（今回はゴールにたどり着くことすらできませんでしたが。）しかし、一般的には完全に正しい予測コストを求めるのは無理だと思われます。第一、そのような場合には探索をするまでもなく他のもっといい方法がありそうですね。

また、他にも最良優先探索は山登り法と同じ情報だけを利用していながら、山登り法の解けなかった問題を解いています。分岐限定法は最適経路を求めていますが、結果としてすべての節点を展開して調べています。

Ａ＊アルゴリズムは最良の解をもっとも速く求めていますが、探索に用いている情報の量も一番多いので、当然といえば当然かもしれませんね。