ファジィ推論と制御のプログラミング

参考書、教科書などには、実際のプログラミングについてはあまりのっていないので、ここでは、ファジィ推論やファジィ制御のプログラムを作る際のヒントになりそうなことをまとめてみたいと思います。ただ、プログラミングについてはあまり詳しくないので技術的には稚拙な部分があるかと思います。（言語はＣ言語を想定しているので、他の言語を使っている方は適宜読み替えてください。）

アルゴリズム化

ファジィ推論やファジィ制御のプログラミングをするに当たって、まずはプログラムとして組み立てるためのおおざっぱなアルゴリズムを考えます。ファジィ制御は複数のIF-THENルールを組み合わせた、ファジィ推論の応用と言えるので、まずは、簡単なファジィ推論を考え、これを組み合わせて行くことでファジィ制御のプログラムが作れそうです。

そこで、アルゴリズム化する際の問題点をリストアップしてみます。

ファジィ集合をどうやって表現するか
AND演算、OR演算はどうするか
重心（非ファジィ化）の計算はどうするか

この３点が解決できれば、プログラム化できそうです。具体的には、ファジィ集合を使って、入力に対するグレードを計算し、これに対してAND/OR演算を行うことで推論を行い、最後に後件部集合を重ね合わせたものの重心を取ることで非ファジィ化が行えるので、一意の答え（具体的数値）として解が求められそうです。

ファジィ推論やファジィ制御の項も参考にしてください。

ファジィ集合の表現

計算機上でファジィ集合を使うためには、入力（横軸）に対して、グレード（縦軸）の値を返す必要があるわけですが、これを関数（またはサブルーチン）として用意できれば便利です。

ファジィ集合はメンバーシップ関数に対して横軸の値を入力することでグレードが求まるものなのでy=f(x)としたいところですが、一般に用いられる三角ファジィ集合や台形ファジィ集合は不連続関数なので少し工夫が必要です。

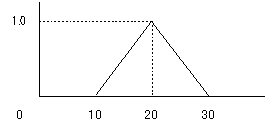
図１　ファジィ集合

図１のようなファジィ集合を扱う場合、式を４本に分けて考えると計算機上でも実現できます。つまり、10より小さい部分、10と20の間、20と30の間、30より大きい部分の４つです。こうすることで、それぞれの部分については簡単な式で表せるのでプログラム化することができます。式で表すと以下のようになります。

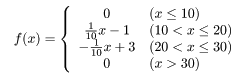
つまり、図２のようにファジィ集合を４つの別々なものと考えれば、簡単に式として表現できるためプログラム化も容易になるわけです。

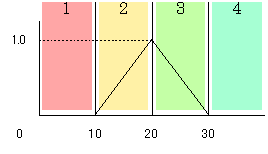
図２　ファジィ集合の分解

したがって、以下のような関数として表現できます。

double fuzzyset ( double value ) {
	double grade;
	if ( value <= 10.0 ) {
		grade = 0.0;
	}
	else if ( value <= 20.0 ) {
		grade = 0.1 * value - 1.0;
	}
	else if ( value <= 30.0 ) {
		grade = -0.1 * value + 3.0;
	}
	else {
		grade = 0.0
	}
	return ( grade );
}

この関数に横軸の値を渡してやるとそのグレードを返す機能を持たせたわけですからあとは、何回でも呼び出して、その都度グレード値を求めることができます。

AND/OR演算

推論を行うには、IF-THENルールの前件部の計算を行うためにAND演算やOR演算が必要になりますが、これも関数として実現しておくとあとで楽になります。ファジィ制御ではAND演算がほとんどですが、ファジィ推論ではOR演算も重要になります。

IF A and B THEN C

という、ファジィ推論を行うには、ファジィ集合AとBのグレードを求めて、その小さいほうのグレードを新たにファジィ集合Cのグレードにしてやればいいので、単純にAとBのグレードを比較して小さい方を（OR演算なら大きい方を）返してくれる関数を作ればいいわけです。（わざわざ作る必要もないかも知れませんがここはあえて作ってみました）

double AND ( double a , double b ) {
	if ( a > b ) {
		a = b;
	}
	return ( a );
}

double OR ( double a , double b ) {
	if ( a < b ) {
		a = b;
	}
	return ( a );
}

これで前件部までできました。あとは、ここで求まった各グレードを持った後件部集合の和（重ね合わせたもの）の重心をとれば推論は完成です。

重心を求める（非ファジィ化）

重心の求め方は推論法が、Min-Max法、代数積-加算-重心法、簡略化推論法かによって異なりますが、簡略化推論法についてはファジィ制御でも扱ったので、ここではMin-Max法の重心の取り方について考えてみたいと思います。

一般的な参考書などを見ると、Min-Max法の重心の取り方は、

となっています。しかし、このままでは連続値の式なので離散値を扱うように変更しなくては計算機上で計算することができません。そこで、後件部ファジィ集合の離散化を行います。例えば後件部ファジィ集合が図３のように big･middle･small のファジィ集合だったとして、これを離散化して行く方法を考えます。

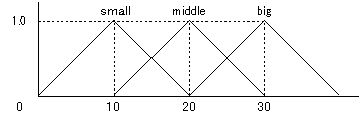
図３　後件部ファジィ集合

推論結果の重心を求めるわけですから、どんな形の合成結果でも重心を求められる必要があります。そこで、各ファジィ集合を図４のように、一定間隔で離散化してやります。

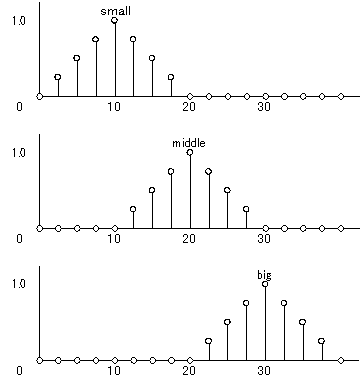
図４　離散化した後件部ファジィ集合

この例の場合は 2.5 間隔で離散化を行いました。こうして考えると、0 から 40 までの間で、2.5 刻みでそのファジィ集合の取りうる最大値のデータ列によってそのファジィ集合が表せるといえます。つまり、言い換えると刻み幅を変えても、そのファジィ集合を表す関数（メンバーシップ関数）があれば、容易に離散化したファジィ集合を得ることができます。

この例では、横軸は 2.5 刻みで、

small  = { 0 0.25 0.50 0.75 1.00 0.75 0.50 0.25 0 0 0 0 0 0 0 0 0 }
middle = { 0 0 0 0 0 0.25 0.50 0.75 1.00 0.75 0.50 0.25 0 0 0 0 0 }
big    = { 0 0 0 0 0 0 0 0 0 0.25 0.50 0.75 1.00 0.75 0.50 0.25 0 }

となります。ということは、重ね合わせるには、横軸が同じ部分のデータについて、比較して大きい方をとれば、いわゆるOR演算ができるわけです。このまま重ね合わせると図５のようになります。

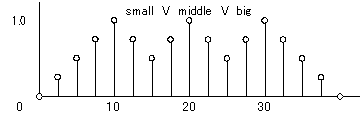
図５　離散化ファジィ集合の合成

ただし、実際に合成して（ORをとって）重心をとるのは、各ファジィ集合にグレードが与えられて、頭きりが起きている状態です。つまり、グレードに従って、各ファジィ集合の高さを変える必要があります。これは、各ファジィ集合のデータ列とそのファジィ集合に与えられたグレードを比較して小さい方をとれば（AND演算をすると）グレードを持ったファジィ集合が得られます。

例えば、

small  = 0.25
middle = 0.75
big    = 0.50

という、グレードが与えられたとすると、各ファジィ集合は図６のようになります。また、その合成結果は図７のようになります。

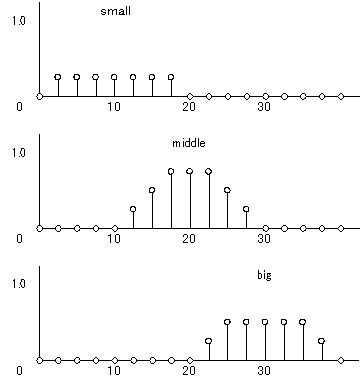
図６　頭きりをした離散化ファジィ集合

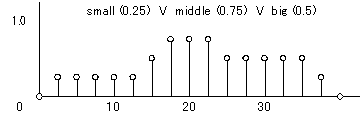
図７　頭きりをした離散化ファジィ集合の合成

そして、最後にその重心を求めるわけですが、ここまで来るとこれは簡略化推論法の後件部と同じファジィシングルトンで集合が表されているため、同じ方法で重心を求めることができます。（ファジィ制御の項も参考にしてください）今回のデータ列は17個なので、

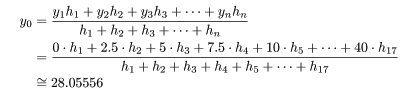
となります。

さて、これでプログラム化ができるようになったわけですが、データ列の取り方や演算方法はいろいろ考えられるので、１例だけ挙げてみたいと思います。

配列 set_small にファジィ集合 small のデータ列が、変数 grade_small にそのグレードが格納されているとすれば、以下の for文でファジィ集合 small の頭きりが行えます。

	for ( i = 0 ; i <= 16 ; i++ ) {
		set_small[i] = AND( set_small[i], grade_small );
	}

ここまでで、図４の状態です。

次に、ファジィ集合の合成には、OR演算を使います。
配列 set_middle,set_big はそれぞれのファジィ集合のデータ列を示します。また、合成したファジィ集合のデータ列は、配列 set_synthesis に格納します。

	for ( i = 0 ; i <= 16 ; i++ ) {
		set_synthesis[i] = OR( set_small[i], set_middle[i] );
		set_synthesis[i] = OR( set_big[i], set_synthesis[i] );
	}

これで、図７のファジィ集合が、配列 synthesis の中に格納されました。

最後にこのファジィ集合の重心をとります。
変数 center に重心を格納することにします。変数 size には刻みに応じた横軸の値が順番に代入されています。（ 0, 2.5, 5, 7.5, 10, ... ）また、変数 num,den は途中計算に使った変数です。

	num = 0.0;
	den = 0.0;
	size = 0.0;
	for ( i = 0 ; i <= 16 ; i++ ) {
		num = num + set_synthesis[i] * size;
		den = den + set_synthesis[i];
		size += 2.5;
	}
	
	if ( den != 0.0 ) {
		center = num / den;
	}
	else {
		center = 0.0;
	}

これで、先程の式の計算ができました。num,den を利用して分子と分母を先に求めて、あとで分子を分母で割ることで求めています。なお、num/den を行うときにif文を使っているのは、分母が 0 の時に割り算を行ってエラーを出さないようにするためです。

以上でファジィ推論（または制御）のためのプログラムは作れると思いますが、この方法よりも、もっと巧く求める方法はいろいろあると思いますので、ぜひ考えてみてください。

2000/12/14