4.AND/ORグラフとゲーム木
問題表現の特殊化限定された問題を扱いたいような場合には、その問題に合わせて問題の表現法を特殊化して行くことで、より簡単に問題を扱うことができます。
AND/ORグラフ複雑で解くことが難しい問題でも、より簡単な部分問題に分解していくことで、その部分問題は解くことができるようになります。AND/ORグラフでは問題を条件によって分解してその状態を表現することができます。
AND/ORグラフには、AND節点とOR節点の2種類の節点があります。AND節点は、その節点に繋がる子節点が全て満たされなくてはならないということを表し、OR節点は、その節点に繋がる子節点のうちどれか一つが満たされれば良いということを表します。
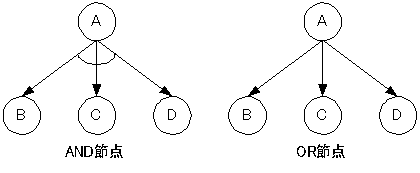
図4.1 AND節点とOR節点
図4.1の例なら、AND節点の場合、Aが成り立つにはB,C,Dが成り立つ必要があります。OR節点の場合は、Aが成り立つにはB,C,Dのうちのどれか一つが成り立てば良いということになります。
AND/ORグラフを利用すると様々な問題を表すことができます。例えば、東京から大阪へ行く経路を探すといった場合、新幹線、飛行機、車など様々な選択肢が選べますが、これらはOR節点で表すことができます。また、飛行機を選んだ場合、羽田空港へ行く、飛行機に乗る、大阪駅(または目的地)へ行く、という3つの節点のANDで表されます。
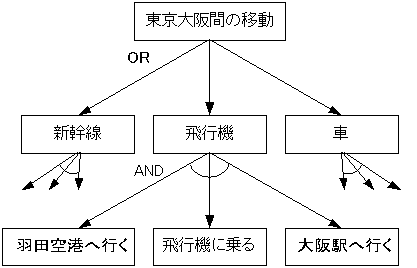
図4.2 東京大阪間の経路
このように、様々な問題はANDとORの条件の組み合わせによって表すことができます。
ゲーム木ゲーム木では、完全ゲームと言われる種類のゲームを扱うことができます。完全ゲームとは、2人で交互に手を指し、最終的に、勝ち、負け、引き分けとなるようなゲームをいいます。例えば、チェッカー、チェス、将棋、囲碁などがこれにあたります。ただし、判定に確率的要素が含まれるような場合には不完全ゲームといいます。サイコロをふるようなゲームがこれにあたります。
ゲーム木では、それぞれの手を打った状態ごとに節点とする木の形で構成されます。(図4.3)
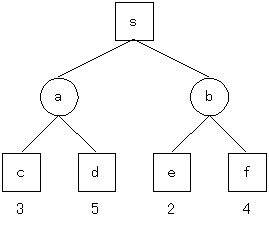
図4.3 ゲーム木
このゲーム木はsが初期状態、次の丸の節点が自分の取りうる手、その次の四角い節点が相手の取りうる手を表しています。そして、最後の四角い節点の下にある数値はその節点(四角)においての自分の評価(どのくらい有利か)になります。
つまり、このゲーム木の場合、現在は自分の手番でaまたはbの手を取ることができ、aを取った場合には、相手はcまたはdの手を取ることができ、自分がbを取った場合には相手はeまたはfの手を取ることができるという状態を表しています。
ただし、ここで各状態ごとに盤面の評価が行えないとゲーム木は成立しません。つまり、将棋などで、ある程度指したあとの盤面をいきなり見てもどちらが有利かを判定することができるということがゲーム木を使う条件になります。
それでは、具体的な方法について説明します。
ミニ・マックス法ミニマックス法は非常に単純な考え方で、相手がこちらの一番不利になる手を打ってくるとして、自分が打てる最良の手を探すアルゴリズムです。つまり、相手は評価をMINにする手、自分はその中で評価をMAXにする手を選ぼうというものです。
では、図4.3の例で考えると、自分が選べるのは丸の節点で四角の節点は相手が選んできます。そこで、自分がaの手を選んだとすれば、相手はその状態から選べる手(c,d)の中でこちらの評価がMINになる手を選んで来ると考えます。したがって自分がaなら相手はcです。また、自分がbなら相手はeです。こうなると、cの評価値は3、eの評価値は2なので、自分はaを選んだほうがよいという結論になります。
このように、先読みと盤面評価を行って行くのがゲーム木です。自分がどんな手を打てるのか、それに対して相手はどう応じて来るのか、その時どちらが有利か、といったことを調べて行くことで最良の手を探します。
当然、先読みの深さを大きくしていくほど強いアルゴリズムになるでしょう。この例では、自分の手に対する相手の次の1手までしか考えていませんが、さらにその手に対して自分の打てる手、それに対して相手の打てる手の評価まで行っていくという方法が考えられます。
しかし、ミニマックス法ではすべての節点についての評価値を求めますから、先読みを深くしていくと、計算量は指数関数的に増えて行ってしまいます。木構造の全てを調べるわけですから、木が大きくなれば、計算量は当然ネズミ算式に増えてしまいます。そこでミニマックス法を改良し、計算量を抑えたアルファ・ベータ法があります。
アルファ・ベータ法この方法はミニ・マックス法と基本的に同じ考え方で、相手は常に一番有利な手を打って来ると考えますが、その上でこれ以上は考えても自分にとって不利な手しか出てこないような枝については、省略して行くという方法です。
ゲーム木がある程度大きいとこのような状況がたくさん出てきます。そこで、盤面の評価を行いながら木を掘り進めることで、余計な枝について評価や探索を行うことを防ぎます。図4.4のゲーム木についてアルファ・ベータ法を考えてみます。
※かなり解かりにくいです。
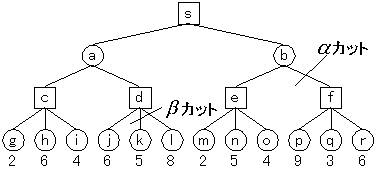
図4.4 アルファ・ベータ法
図中にベータカット、アルファカットとありますが、この例ではアルファ・ベータ法により、ここから先の探索を省略できます。左側から順に探索を行うとして、まず、a,cと来て、g,h,iについて探索を行い、この選択は自分の手の選択ですから、一番評価の高くなるようにhを選択するので、したがって、cの節点の評価はhの評価である6となります。(つまり、自分がaを選び相手がcを選んだなら、その次には自分がhを選ぶのが最良なのでその時の評価である6が、相手の手であるcの評価であるといえます。)
次に、cの評価はわかったので、dの評価についても調べます。そこで、dのあとに選べる手である、j,k,lの評価を行いその中で一番いいものがdの評価と言えるわけですが、jを調べるとその評価は6とわかります。これはhの評価と等しく、この時点でk,lについて探索を行う必要がなくなります。なぜなら、もしもk,lのどちらかの評価がjよりも高かったなら、相手はcかdかを選択する時点でdを選ぶことは明らかに損ですから、cを選んで来るだろうと予想できます。逆にk,lどちらの評価もjよりも低かったとしたら、相手がdを選んできた場合、自分はjを選べば一番有利だと予想できます。これが、ベータカットです。
これで、aを選べば、そのあと相手がどんな手を取ってこようとも、その後の自分の手による評価は、最高でも6であるとわかります。
次にb以下を調べるわけですが、eの子節点であるm,n,oについて探索を行い、その最大の評価であるnのときの5がeの節点の評価となります。すると、eかfかの選択は相手の選択なので、f以下にもっと評価の高い手があったとすれば、相手はfを選びませんし、それよりも低い評価ならば相手はfを選んで来るでしょうが、その場合は自分がbの手を選んだときの最高の評価はさらに低いことになります。ということは、自分がbを選んだ場合の評価は相手がeを選んだときの5より高くなることはあり得ないことが予想できます。
それならば、はじめに自分はaを選んでいれば、評価6の手を得ることができるので、少なくともbの手を選ぶよりは得であると考えられます。この時点でb以下の手についてこれ以上調べる必要が無くなるため、f節点以下の探索を行う必要が無くなります。これがアルファカットです。
ベータカットは、相手の手に続く自分の手について、調べる必要のないものをカットすることができます。その条件は、はじめに調べた相手の手の節点(c)以下で、もっとも評価の高い節点(h)の評価を仮に、その親の親の節点(a)である自分の手の評価とし、その子節点(ここではdだけだが、もっとたくさんあってもよい)については、その下に評価が先程の仮の値(hの評価である6)と等しいか大きかった時点で(jの評価=6)その節点(d)以下については、それ以上の探索を打ち切る(ベータカットする)ことができます。
アルファカットは、自分の手に続く相手の手について、調べる必要の無いものをカットすることができます。その条件はすでに自分の手について一つ以上評価を調べているとき、(aならば6)自分の手(b)の子節点である相手の手(e,f)については、その評価が等しいか低い節点が見つかった(eの評価5はaの評価6より小さい)時点で、その兄弟の節点(ここではfだけだが、もっとたくさんあってもよい)についてそれ以上の探索を打ち切る(アルファカットする)ことができます。
アルファカットもベータカットも条件に評価が「等しい」場合を含めて打ち切っていますが、これは、先読み(探索)をある一定の深さまでしかしないため、その深さまでで等しければ、どちらを選んでも結果は同じであると考え、初めに見つけたほうを採用しているためです。